CRYSTAL
TUTORIAL
Localization
of Transition States with CRYSTAL09
A. Rimola and C. M. Zicovich-Wilson
1. Introduction
2. Mathematical definition of
Transition State
3.
The adopted strategy: Distinguished Reaction Coordinate. Example: keto-enol
tautomerization of formamide.
i) Defining a geometry close to a TS
ii) Geometry optimization of a TS
4. Key
features
i) Initial Hessian matrix guess: Numerical estimate or
classical model?
ii) Energy tolerance
iii) Preliminary calculations using less time consuming
methods
iv) Additional options to follow the direction of maximum
energy
5.
Other examples
i) Amide bond formation
ii) Proton jump in the H-exchanged aluminosilicates
a) H-Edingtonite
b) H-Chabazite
6.
Acknowledgements
1. Introduction
An
“optimized structure” corresponds to a minimum point on the potential energy
surface (PES) (the potential energy is the sum of electronic and nuclear
repulsion terms resulting for a given Hamiltonian). Usually, the optimized
structure is located by means of a “minimization” algorithm and it may refer
either to minima or to transition state (TS) structures. Indeed, minima
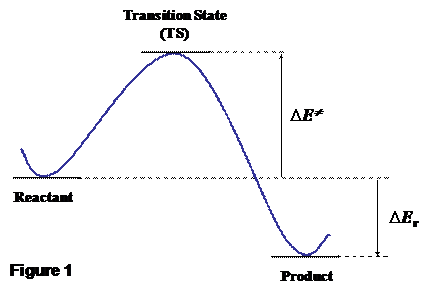
structures (i.e. reactant/intermediates/products) only provide thermo-chemical data for a given reaction, from which reaction
energies are arrived at (DEr, see Figure 1).
However, reactions exhibiting very favorable DEr
values may occur very slowly. For instance, at variance with the very large DEr» -2800 kJ mol-1
value for the combustion of glucose by O2 to give CO2
and H2O, the energy barrier (DE≠) that separates reactants from products is very high, thus hindering sugar to spontaneously burn in air (see Figure
1). Technically speaking, it is said that, whereas the reaction is “thermodynamically
favored” it is also “kinetically hindered” due to the high DE≠. Clearly, the knowledge of the correct DE≠ value is as important as that of the reaction energy (DEr) to
accurately model chemical reactions, so that
efficient algorithms are needed to locate the TS structures on the PES. For
a given reaction, a TS corresponds to a maximum
energy structure connecting reactants and products to each other. Obviously,
locating TS allows to compute DE≠ values easily (for
the forward reaction is the energy difference between TS and reactants). Therefore,
when all minima and TS structures have been located, both thermodynamic and
kinetic data are at hand so that the full energy profiles can be derived by
means of quantum chemical calculations (Figure 1).
|
|
2. Mathematical
definition of Transition State
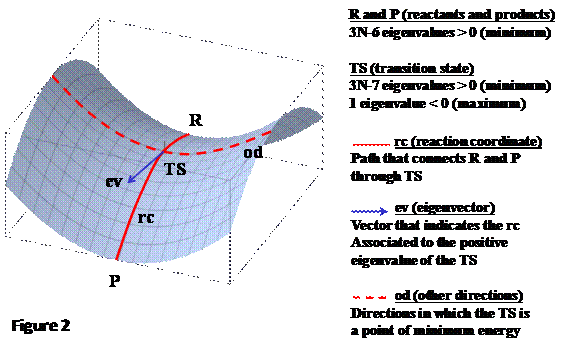
Points
of interest on the PES are called “stationary points” which are characterized by
a zero value of the gradient ![]() vector (first-derivatives
of the energy).
vector (first-derivatives
of the energy).
![]()
Reactants, products and intermediates, all of them are
stationary points of the PES with the same mathematical properties as are TS
structures which can be distinguished from minimum structures by the the
Hessian matrix H features (second-derivatives
of the energy). Once the H matrix is
computed it is then diagonalized (D matrix) by an unitary P matrix with the signs of the resulting eigenvalues {![]() } revealing the mathematical nature of any stationary
point.
} revealing the mathematical nature of any stationary
point.
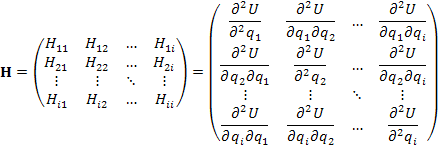
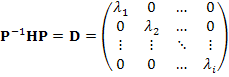
The eigenvalues define the harmonic vibrations whose
normal modes are the corresponding eigenvectors contained in the P matrix. It is worth remembering that,
for a non-linear molecule envisaging N
atoms, 6 of the 3N eigenvalues are
equal to 0 because 3 translations and 3 rotations have obviously zero
vibrational frequency. If a stationary point has the remaining 3N-6 eigenvalues all positive then the
point is a true minimum in any direction
of the PES (any movement in whatsoever direction will increase the energy), so
that this point corresponds to either reactant, product or intermediate
structures. On the contrary, if a stationary point has 3N-7 eigenvalues positive and only
one negative value then the point is called a “saddle point” (a minimum of
energy in every directions of the PES but for one in which it is a maximum of
energy). This point corresponds to a TS structure, and the direction by which
the TS is a maximum in energy connects the reactants with the products (the so called
“reaction coordinate”). Additionally,
the eigenvector associated to the negative eigenvalue gives the direction of the
reaction coordinate on the PES. Figure 2 summarizes these concepts.
|
|
The difficulty when locating TS structures arises from
the fact that they are minima in 3N-7
directions of the PES and a point of maximum of energy along the direction that
governs the reaction. Whereas for reactants, products and intermediates full
minimization at every direction is required, for TS the maximization in one
direction is also needed.
3. The
strategy adopted: Distinguished Reaction Coordinate. Example: keto-enol
tautomerization of formamide
The need to maximize the energy in one (and only one)
direction, hence finding a
transition state on a PES, is a very delicate process because roughly guessed attempts
to locate a TS usually lead to unsuccesfull results. In standard molecular quantum
mechanical codes, a lot of experience and ingenuity has been devised to code
very successful and efficient algorithms to locate saddle points on the PES. One should
also realize, however, that even nowadays not very many codes are capable to
handle TS search and characterization (Gaussian03 as a notable exception).
Usually periodic codes based on
plane waves pseudo-potential approach adopt the nudged elastic band (NEB)
approach (H. Jónsson, G. Mills, K. W. Jacobsen, Nudged Elastic Band Method for
Finding Minimum Energy Paths of Transitions, in Classical and Quantum Dynamics
in Condensed Phase Simulations, Ed. B. J. Berne, G. Ciccotti and D. F. Coker,
385 (World Scientific, 1998)). The NEB has the advantage of requiring energy
and gradient only to discover the minimum energy path, at the expense of a
relatively high number of images needed to improve the accuracy of the
search. The strategy adopted by CRYSTAL09
to locate TS is different from NEB and it is called the distinguished reaction coordinate (DRC) and its
coding has been inspired by similar approaches adopted by molecular programs.
As it is customary for CRYSTAL09 algorithms, DRC can be successfully used for systems of any
dimensionality (molecules, polymers, slabs and crystals). DRC divides the TS
search in two successive steps: i)
defining a structure as close as possible to the TS; ii) refine this structure
to exactly locate the actual TS. These two steps are described below and are
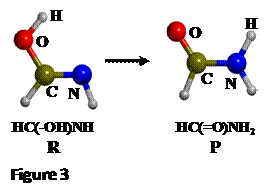
exemplified by the keto-enol tautomerization of formamide (HC(-OH)NH -->
HC(=O)NH2, see Figure 3). For this reaction, calculations were
performed with the B3LYP functional using a standard double-zeta polarized
basis set.
|
|
i)
Defining
a geometry close to a TS.
To do that, a scan calculation
along the internal coordinate that governs the reaction should be performed. This
scan calculation consists in evolving, step by step and in a controlled way,
the selected internal coordinate so to move from reactants to products by
crossing a point of maximum energy. Looking at our example, the tautomerization
involves transferring a proton attached to the O atom (OH) in the reactant to
the the N atom (NH) in the product, so that we can consider the H-N distance as
the internal coordinate that drives the reaction (see Figure 3). Thus the H-N distance will be our
distinguished reaction coordinate (or simply, reaction coordinate). The scan
calculation evolves the reactant geometry towards the product in many steps along
the reaction coordinate (the H-N distance shorten from R towards P). At each
step, the value of the reaction coordinate is frozen while all other internal
coordinates are relaxed, so a ‘pseudo-optimized’
structure is computed. At the end of the scan calculation, a set of
intermediate energy points connecting reactants and products (defined by the various
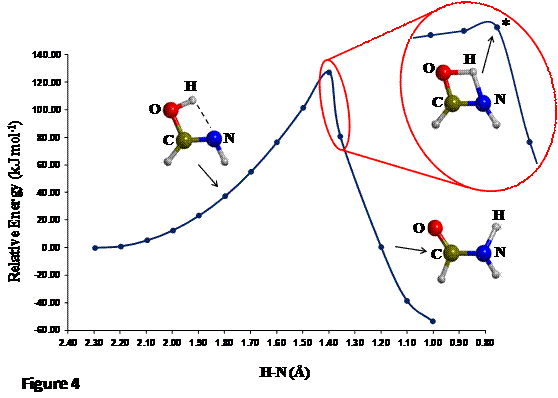
‘pseudo-optimized’ structures) is obtained. Focusing on our example, the H-N
distance is scanned from the initial value of
2.3 Å (the value for R) to a final value of 1.00 Å, with 14 pseudo-optimized
structures each displaced by a step of -0.1 Å (the minus sign means shortening). The
energy variation as a function of the distinguished reaction coordinate for the
tautomerization is shown in Figure 4.
|
|
The distinguished energy profile exhibits three different zones: i) a zone
where the energy moderately rises as the H-N distance becomes shorter
(reactant-like zone, because the O-H bond has not been broken yet); ii) a zone
where the energy is quite high and goes through a maximum (TS-like zone, because
the H is almost midway); iii) a zone where the energy decreases notably
(product-like zone, because the H is attached to N). The most important structure
of this distinguished energy profile is the one at the maximum of energy as its
geometry defines the initial guess for the next step: the accurate TS geometry localization.
If a more accurate initial guess geometry for the TS is desired, one can
perform a second scan calculation with shorter steps (zone inside the red
circle of Figure 4), around the maximum energy zone (i.e. between 1.4 and 1.3 Å).
Proceeding like that, a maximum energy structure (labelled with asterisk in
Figure 4), is chosen to be the initial guess for the TS optimization.
From the practical point of view,
the scan calculation is performed by CRYSTAL09 via a number of keywords to be
specified in the geometry input block:
-
INTREDUN: defines and optimizes the geometry in internal coordinates (bond lengths,
angles and dihedral angles). It is mandatory
for scan calculations
|
INTREDUN |
Optimization is performed in
internal coordinates |
-
LNGSFROZEN or ANGSFROZEN:
To define the frozen bond lengths or angles apt to define the DRC. Several
values can be frozen. For the simplest case in which only one distance is frozen
the input reads as:
|
LNGSFROZEN 1 5 2 0 0 0 |
A bond length is frozen Number of bonds to be frozen. Atom_1 and atom_2
define the bond atom_1 | atom_2 | Cell index* where the atom_2 is
located |
* This is important in order to
avoid pitfalls when the DRC involves atoms belonging to different crystallographic
cells.
-
SCANREDU: performs the scan calculation on one of the internal coordinates
defined in LNGSFROZEN or ANGSFROZEN. For the scan of a bond length, the input reads
as:
|
SCANREDU 1 1.0 14 |
performs a scan calculation Bond length* | final value (Angstrom) | number of steps |
*Bond lengths are defined by
number 1, angles by number 2
The corresponding sections of the
CRYSTAL09 output are highlighted here:
|
N OF INTERNAL COORDINATES: 33 N OF ALLOWED
DEGREES OF FREEDOM: 12 (INTERNAL+CELL
PARAMETERS) BOND LENGTHS
(L), ANGLES (A) AND DIHEDRALS (D), THEIR VALUES (IN ANGS AND DEGREES),
MULTIPLICITIES AND WHETHER COORDINATE IS FROZEN(T) OR NOT(F). NUM, ATOM LABELS AND CELL INDICES OF THE
POINTS VALUE MUL FRZ (L) 1 5 H
2 N ( 0 0 0) 2.2958 1 T 2 2 N
1 C ( 0 0 0)
1.2677 1 F 3 3 H
1 C ( 0 0 0)
1.0946 1 F 4 4 O
1 C ( 0 0 0) 1.3473 1 F … |
This block appears when INTREDUN and LNGSFROZEN are included. For the sake of brevity, here only the
first four internal coordinates are shown, which correspond to distances.
Information about which internal coordinate is frozen (true, T) or free to
relax (false, F) is also provided. In this case, the internal coordinate number
1 defined by atoms 5 and 2 is frozen to 2.2958 Å (highlighted in yellow). The SCANREDU keyword, is summarized below:
|
SCAN ALONG PARAMETER 1. FIRST POINT OUT OF 14 UP TO
VALUE 1.00000 WITH STEPS OF -0.09968 |
The scan calculation will be
performed along the first internal coordinate (parameter 1, defined previously
by INTREDUN and LNGSFROZEN) and takes 14 steps up to a value of 1.0 Å with a
step size of -0.09968 Å. The evolution along the scanned coordinates is
highlighted in the CRYSTAL09 output as following:
|
SCAN POINT
2 OUT OF 14 … SCAN POINT
3 OUT OF 14 … SCAN
POINT 4 OUT OF 14 … |
When a given step of the scan
calculation (here is reported the second step) finishes, a final summary of the frozen parameter (T)
and the relaxed ones (F) is printed:
|
MAX
GRADIENT 0.000297 THRESHOLD 0.000450 CONVERGED YES RMS
GRADIENT 0.000097 THRESHOLD 0.000300 CONVERGED YES MAX
DISPLAC. 0.001404 THRESHOLD 0.001800 CONVERGED YES RMS
DISPLAC. 0.000622 THRESHOLD 0.001200 CONVERGED YES CONVERGENCE
TESTS SATISFIED AFTER 6 ENERGY AND
GRADIENT CALCULATIONS ****************************************************************** * OPT END -
CONVERGED * E(AU):
-1.697836059008E+02 POINTS 6 * ****************************************************************** FINAL SET OF
INTERNAL COORDINATES BOND LENGTHS
(L), ANGLES (A) AND DIHEDRALS (D), THEIR VALUES (IN ANGS AND DEGREES),
MULTIPLICITIES AND WHETHER COORDINATE IS FROZEN(T) OR NOT(F). NUM, ATOM LABELS AND CELL INDICES OF THE
POINTS VALUE MUL FRZ (L) 1
5 H 2 N ( 0 0 0) 2.1962 1 T 2
2 N 1 C ( 0 0 0)
1.2674 1 F 3
3 H 1 C ( 0 0 0)
1.0938 1 F 4
4 O 1 C ( 0 0 0) 1.3445 1 F |
.
When the scan calculation
finishes properly, a summary like this is printed.
|
SCAN SUMMARY PARAMETER
RELATIVE ENERGY (KJ/MOL) ----------------------------------------------------------------- 2.295800 0.00000000000 2.196155 1.04289520376 2.096492 5.32369577437 1.996829 12.6683675254 1.897175 23.2618645741 1.797445 37.3571946894 1.697780 55.0603586276 1.598127 76.5376596033 1.498437 101.353780940 1.398896
127.201803874 1.356055 80.8585460765 1.199789 0.600313775081 1.100189 -38.4335531862 1.001133 -53.3049264802 ----------------------------------------------------------------- |
The value of the internal
coordinate along which the scan was carried out is shown along with the
relative energy (the first step chosen as a zero reference) of each ‘pseudo-optimized’ structure for each step. Here,
the highest energy structure obtained along the scan belongs to the structure
with a distance of 1.398896 Å (highlighted in yellow). From this structure we can try to
obtain an optimized TS structure (see below, section ii).
The input and output files of the
first and second scan calculations addressed to the proton transfer in the
keto-enol tautomerization of formamide are available here:
keto-enol-SCAN1.d12 and keto-enol-SCAN1.out
keto-enol-SCAN2.d12 and keto-enol-SCAN2.out
ii)
Geometry
optimization of a TS
When the scan calculation is
accurate enough, then the structure of maximum energy is the one that is very
close to the actual TS and will serve as an initial guess to accurately reach
the TS. To ensure that the algorithm will follow the right direction along
which to maximize the energy it is mandatory to first compute the Hessian
matrix. CRYSTAL09 can compute an initial Hessian matrix via numerical estimate
(very accurate but expensive) or through models based on the Schlegel scheme
(cheaper but less accurate). Our experience shows that both methods bring to TS
structures; however, for cases in which TS structures are rather complex, the numerically
estimated Hessian provides a more robust path to locate the final TS.
Additionally, since the Hessian matrix is computed by numerical evaluation of the first analytical derivatives
of the total energy it is highly
recommended to tighten the SCF energy tolerance (10-11 Hartree) to
ensure good numerical accuracy. More discussion on this point will be found in
section 4 of ‘Key Features’ (see below).
The starring keyword for a TS
search is TSOPT, and should be
inserted in the geometry input block. This keyword must superseed any Hessian
updating scheme available for full minimisation (i.e. BFGS, OLDCG or POWELL), otherwise calculation will revert
to a standard minimum structure optimization.
|
TSOPT |
Perform geometry
optimizations to a TS |
Accordingly, by inserting, as the
initial guess, the geometry of the highest energy ‘pseudo-optimized’ structure resulting
from the scan calculation the TSOPT keyword will initiate the calculation for a
TS.
CRYSTAL09
generates, by default, an initial Hessian by means of a classical model
proposed by Schlegel (HESSMOD2). If
a numerical estimate of the initial Hessian is desired, in the geometry input block
HESSNUM must be inserted. As already
explained, in the Hamiltonian and SCF control input block the energy tolerance should
be set to 10-11 Hartrees.
|
HESSNUM |
Compute a numerical estimate of the Hessian
(in input geometry block) |
|
TOLDEE 11 |
Control the SCF energy tolerance convergence. Energy tolerance of 10-11 Hartrees
(in input SCF and parameters control block) |
Proceeding like this, the TS for
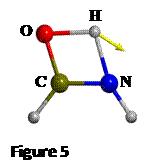
the keto-enol tautomerization has been found (see Figure 5), with a H-N
distance of 1.335 Å, which lies between 1.4 and 1.3 Å as the scan calculation
predicted. Having the energies of R, P and TS, the reaction energy and the
activation energy of the reaction resulted in DEr -53 kJ mol-1 and DE≠ = 139 kJ mol-1
respectively.
|
|
To ensure that the located TS is
indeed so, a full harmonic frequency calculation should be carried out which
should give one imaginary frequency associated to the reaction path (n≠, so-called transition frequency). For the keto-enol
tautomerization, n≠ = 1906i cm-1
is rather high and consistent with the proton transfer. Additionally, by
frequency calculations of R and P thermodynamic data can be computed giving
enthalpy and free energy values at T= 298 K by means of static
calculations: DHr(298) = -55 kJ mol-1,
DGr(298)
= -57 kJ mol-1, DH≠(298) = 127 kJ
mol-1 and DG≠(298) = 121 kJ
mol-1.
The input and output of the TS
search calculation are available here:
keto-enol-TS.d12
and keto-enol-TS.out
4. Key
Features
i) Initial Hessian matrix: Numerical estimate or
classical model?
As mentioned above, with the TSOPT option CRYSTAL09 computes the force constant matrix H of the initial
structure which, by default, is based on the classical model proposed by
Schlegel. As said, the H matrix can also be computed numerically via HESSNUM keyword. Accordingly to our moderate
experience, when a good starting TS guess is provided during the scan, the final
TS is usually located equally well by both methods. This has been, for instance,
the case for the keto-enol tautomerization.
The Schlegel estimate is faster and less accurate so
that many more optimization points are usually requested to locate the TS than
with the more expensive numerical Hessian. It is worth mentioning , however, that the Schlegel
Hessian can in some cases bring some instabilities during the TS search which
may push the geometry of the system far away from the proper TS structure. For
these cases, it is much better to rely on the numerical estimate of the Hessian
matrix.
ii) Energy tolerance
The accuracy of the eigenvectors
and eigenvalues of the initial Hessian matrix
strongly depends on the energy tolerance enforced to achieve SCF
convergence. Once small enough, it ensures that the direction along which to
maximize the energy is accuartely determined. A robust recipe is to set up the
SCF tolerance to 10-11 Hartrees. In contrast, using the default
energy tolerance of 10-7 Hartrees, does not allow to locate the
initial negative eigenvalue so that the direction along which to maximize the
energy is ill defined. The two cases are show here for the keto-enol
tautomerization. The TOLDEE=11 correctly identifies one negative eigenvalue
whose associated eigenvector will be followed to locate the TS. For TOLDEE=7 no
negative eigenvalues are found.
|
TOLDEE 11 |
EIGENVALUES OF THE ESTIMATE HESSIAN -0.9872E-01 0.1055E-01
0.3633E-01 0.5014E-01 0.1114
0.1596
0.1659 0.1948 0.3407 0.4405 0.4766 0.5106 |
|
TOLDEE 7 |
EIGENVALUES
OF THE ESTIMATE HESSIAN 0.2300E-02
0.2301E-02 0.4773E-01 0.1600
0.1600 0.1629 0.1793
0.2078 0.3407 0.4404 0.4559 0.4954 |
To find out the
TS for TOLDEE=11, 13th optimization cycles were needed, which increase to 86th for
TOLDEE=7.
iii) Preliminary calculations using less time consuming
methods
As it is clear the ‘scan
calculation + TS search’ to arrive at the TS structure can be quite time
consuming, particularly when using
hybrid functional for the definition of the exchange-correlation part. A good
strategy to save time is to perform scan calculations and the search of the TS with
more approximate methods (HF or pure GGA) and smaller basis sets (for instance
dropping the polarization functions). Once the approximate TS is located, it
can be used as a better guess for the final TS optimization using the most
expensive method.
This has been done for the
keto-enol tautomerization of formamide using as preliminary calculations the
PBE functional and using it as a guess for the B3LYP level. The final TS coincides with
that resulting from a search entirely based on the B3LYP level at a fraction of
the total cost.
iv) Additional options to follow the direction of maximum
energy
By default, CRYSTAL09 follows the
direction of the eigenvector associated to the smallest eigenvalue of the
Hessian matrix at each point of the optimization process. For each new step the
Hessian matrix is evolved by an updating algorithm which avoid the very
expensive computation of the numerical Hessian to each step. Because the H matrix
changes at each geometrical step there are two possible scenarios: i) one keeps
going along the direction indicated by the eigenvector associated to the
original eigenvalue; ii) a new eigenvalue, smaller than the one computed at the
beginning of the optimization may result from the diagonalization of the new H
matrix defining a new eigenvector and then a new direction to be automatically
followed by CRYSTAL09. To avoid the switch to the new direction the keyword MODEFOLLOW must be inserted in the
input geometry block to freeze the evolution along the original direction, as follows:
|
MODEFOLLOW 1 |
To follow the same eigenvector along all the
optimization Order number of the eigenvector to follow
associated to the eigenvalue. For this
case 1 refers to the smallest one. |
An alternative to follow the direction dictated by the
eigenvector associated to the smallest eigenvalue is to search the TS by
following a path defined by internal coordinates. For instance, the proton
transfer of the keto-enol tautomerization is governed by the H-N distance, so
that one can prefer to follow the internal coordinate of the bond length
defined by the H and N atoms. This can be setup by the PATHFOLLOW keyword, to be inserted in the input geometry block:
|
PATHFOLLOW 5 |
To follow a path based on internal coordinates Order number of the internal coordinate to
follow |
Up to
two different internal coordinates can be used in order to define a path by using
the keyword FITTOPATH to set up the
second internal coordinate in the input geometry block as follows:
|
FITTOPATH 6 40 |
To follow a path Order number (6) of the second internal
coordinate to follow | the weight (in %, 40%) of this internal coordinate in
the path. The missing 60% is represented by the first internal coordinate
specified in the PATHFOLLOW |
5. Other
examples
i) Amide bond formation
The simplest amide bond formation
corresponds to the condensation of formic acid and ammonia to give fomamide and
water:
HCOOH
+ NH3 à HC(=O)NH2 + H2O
The reaction involves two simultaneous processes : i) the
nucleophilic attack of N towards the C of the formic acid; ii) a proton
transfer from NH3 to the OH group of formic acid. Since these two
processes occur in a concerted fashion,
the eigenvector associated to the TS involves the motion of several internal
coordinates.
We
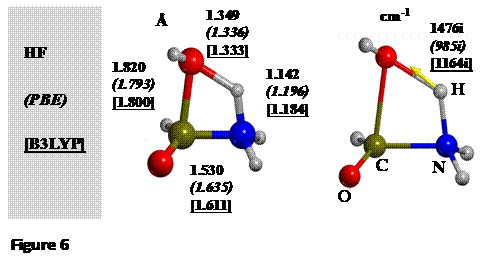
have computed different TS structures, using HF, PBE and B3LYP methods with a
standard double-zeta polarized basis set. The order of calculations is HFàPBEàB3LYP so that the
TS structure from the cheapest method (HF) is used as initial guess for the PBE
level, and this one obtained with PBE serves as initial guess for B3LYP. The
differences are shown below:
|
|
Structural parameters are in reasonable agreement
between different methods, whereas the HF value of the transition frequency,
due to the lack of electron correlation, is much higher than the PBE and B3LYP values.
Similar behavior is shown by the computed DE≠, the HF energy barrier (311 kJ mol-1) being much higher than
those for PBE and B3LYP (204 and 232 kJ mol-1, respectively).
The
inputs and outputs of the TS search calculations are available here.
Reactant structures
abf-HF_REACT.d12
and abf-HF_ REACT.out
abf-PBE_
REACT.d12 and abf-PBE_ REACT.out
abf-B3LYP_ REACT.d12 and abf-B3LYP_ REACT.out
TS structures
abf-HF_TS.d12
and abf-HF_TS.out
abf-PBE_TS.d12
and abf-PBE_TS.out
abf-B3LYP_TS.d12
and abf-B3LYP_TS.out
ii) Proton jump in the H-exchanged aluminosilicates
These examples focus on the
proton transfer occurring in acidic alumino-silicates between different oxygen
atoms belonging to the (Si-O)3-Al(OH) moiety.
a. H-edingtonite
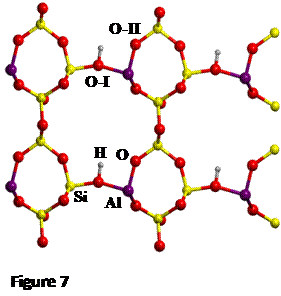
Here H-exchanged alumino-silicate
edingtonite has been chosen as one reference system (structure shown in Figure
7).
|
|
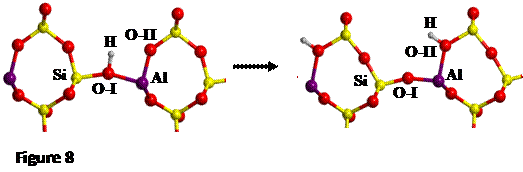
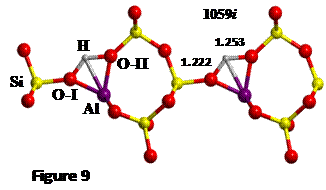
The proton jump between oxygen I and oxygen II (O-I
and O-II, respectively, see Figure 7), in dry conditions, whose initial and
final states are shown in Figure 8, has been studied.
|
|
Calculations were carried out at PBE level with a
standard double-zeta polarized basis set. Here, a scan calculation taking as
distinguished reaction coordinate the distance between H and O-II has been
performed. To save computational time, the scan starts with a distance of 1.8 Å
and when any structure crosses through a maximum of energy then we kill the
job. The TS found is shown in Figure 9, which results in a DE≠= 33 kJ mol-1.
|
|
The inputs and outputs involved on the TS search
calculations are available here.
Reactants: H-edi_REACT.d12 and H-edi_REACT.out
SCAN:
H-edi_SCAN.d12 and H-edi_ SCAN.out
TS: H-edi_TS.d12
and H-edi_TS.out
b. H-Chabazite
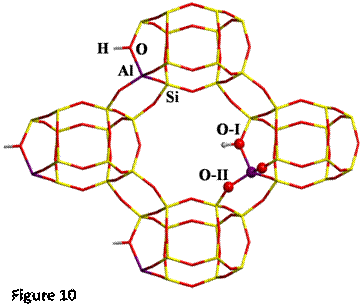
Here H-exchanged alumino-silicate
Chabazite has been chosen as the other reference system (structure shown in
Figure 10).
|
|
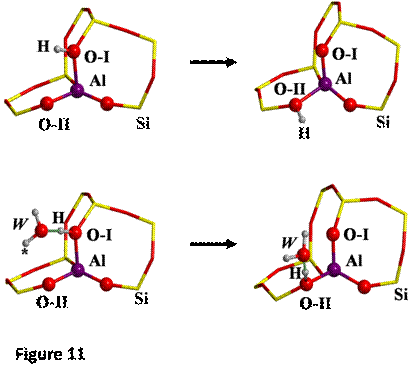
The proton jumps between oxygen I and oxygen II (O-I
and O-II, respectively, see Figure 7), both in dry conditions as well as in
presence of one water molecule, whose initial and final states are shown in
Figure 11 have been studied.
|
|
Calculations were carried out at
B3LYP level with a standard double-zeta polarized basis set. For the dry case,
a scan calculation taking as distinguished reaction coordinate the distance
between H and O-II has been performed. In presence of one water molecule, the
distinguished reaction coordinate was the distance between the H labeled with
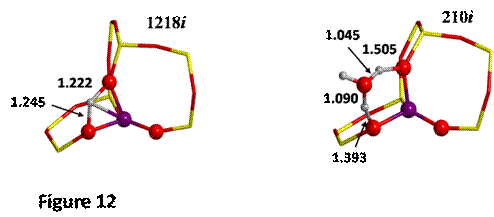
an asterisk (H*, see Figure 8) and O-II. The TS found for each case are shown
in Figure 12.
|
|
|
The computed DE≠ values for the proton jump are 63 and 25 kJ mol-1 for the
dry zeolite and that in presence of water, respectively. This result shows the
catalytic role played by water in the process, which induces a lowering of the
kinetic barrier of 38 kJ mol-1. The lowering is in agreement with
the values of the transition frequencies, higher for the dry case (1218i cm-1)
indicating a very constrained TS (a four atom ring is formed!) at variance with
a much lower value for the case with water (210i cm-1), indicating a less constrained TS (a 6 atom ring
is formed).
Sauer and coworkers have studied the proton jump in
several H-exchanged alumino-silicates, including Chabazite (M. Sierka and J. Sauer, J.
Phys. Chem. B, 2001, 105, 1603). Periodic calculations were carried out adopting the
QM-Pot approach, in which the QM region, (involving the reaction site) was
computed at a B3LYP level combining double-zeta polarized (H, Si and Al) and
triple-zeta polarized (O) basis set, whereas the long range contribution was
handled by molecular mechanics embedding. Their value of DE≠ = 73.6 kJ mol-1 for the proton transfer between O-I and O-II
in dry chabazite. When a triple-zeta polarized basis set was adopted for the
present periodic calculation a value of DE≠ = 73.1 kJ mol-1 was computed, in remarkable agreement with
the Sauer value. The excellent agreement between these two results suggests
that the TS search algorithm implemented in CRYSTAL09 does indeed provide robust
results comparable with those obtained by standard QM molecular packages.
The inputs and outputs involved on the TS search
calculations are available here.
Reactants:
Chab_REACT.d12
and Chab_ REACT.out
Chab-W_
REACT.d12 and Chab-W_ REACT.out
TS:
Chab-W_TS.d12
and Chab-W_TS.out
6. Acknowledgments
We would like to thanks to Prof. Piero Ugliengo (University
of Turin) for the careful and critical reading of this tutorial. AR is indebted
to Ramon Areces Foundation for funding a post-doctoral research project at the
University of Turin during the academic years of 2007/08 and 2008/09.